Há vários anos atrás, trabalhei com o desenvolvimento de jogos para celulares (época de CDMA, TDMA, Brew, Java ME e outros bichos). No começo, não eram jogos muito elaborados, mas sim pequenos jogos casuais. Um deles era um jogo de Poker! Aquele Poker de 5 cartas, com uma rodada de apostas, uma rodada de troca de cartas e uma última rodada de apostas:

Queríamos que o usuário pudesse jogar sozinho, ou seja, contra uma IA (ninguém falava assim naquele tempo 🙂 – se falava “jogar contra o computador”). O nosso desafio era, então, arrumar uma forma de fazer o jogo saber selecionar as cartas que seriam trocadas. Que lógica iríamos usar para fazer uma boa troca de mão?
Foi então que pensamos em usar Aprendizado por Reforço (Reinforcemente Learning), que é uma técnica de Aprendizado de Máquina (Machine Learning) onde o programa tenta realizar diferentes ações verificando o resultado delas: se o resultado for bom, a ação que o causou “ganha pontos” e será realizada mais vezes; caso contrário, a ação “perde pontos” e será realizada menos vezes. Após várias interações, é esperado que o programa aprenda quais ações deve realizar nas diferentes situações.
A inteção deste artigo é a de relembrar os velhos tempos e programar novamente esse algoritmo que sabe fazer boas trocas de cartas em uma mão de Poker. 🙂
Aprendizado por Reforço
Destrinchando um pouco mais a ideia, vamos pensar em quais ações poderíamos fazer na troca de cartas:
- Podemos trocar apenas uma carta – e aí temos 5 opções, sendo desde a 1ª carta até a 5ª carta;
- Podemos trocar duas cartas – a 1ª e a 2ª, a 1ª e a 3ª e assim por diante, até a 4ª e 5ª cartas;
- Podemos trocar três cartas – a 1ª, a 2ª e a 3ª, a 1ª, a 2ª e a 4ª e assim por diante, até a 3ª, 4ª e 5ª cartas.
- Podemos trocar quatro cartas – acho que você pegou a ideia…
- Podemos trocar as cinco cartas – a mão estava ruim mesmo!!!
O último caso é uma dica: nem sempre vamos querer trocar todas as cartas. Nem sempre vamos querer trocar quatro cartas… Como saber qual ação tomar? É aqui que entra o conceito de estados! Se você está no estado de uma boa mão, você não vai querer trocar todas as cartas. Vai depender do que você tem! Vai depender do estado em que você se encontra!
Dessa forma, o que vamos precisar é de um “tabelão” de estados vs ações! Para cada estado em que nos encontramos, temos as possíveis ações que podem ser realizadas e, no cruzamento dessas informações, uma “pontuação”, um “peso”, algo que indique se devemos realizar mais ou menos daquela ação dado um estado qualquer!
| Estados\Ações | Não troca nenhuma carta | Troca a 1ª carta | Troca a 2ªcarta | … | Troca as cartas 1, 2, 3 e 5 | Troca as cartas de 1 a 4 | Troca as cinco cartas |
|---|---|---|---|---|---|---|---|
| Straight Flush | 10 | 0 | 0 | … | 0 | 1 | 0 |
| Quadra | 5 | 19 | 21 | … | … | … | … |
| Full House | … | … | … | … | … | … | … |
| Flush | … | … | … | … | … | … | … |
| Straight | … | … | … | … | … | … | … |
| Trinca | … | … | … | … | … | … | … |
| 2 Pares | … | … | … | … | … | … | … |
| 1 Par | … | … | … | … | … | … | … |
| Maior Carta | 1 | 3 | 2 | … | … | … | 9 |
Veja, se eu tenho um Royal Flush ou um Straight Flush, eu não deveria querer trocar nenhuma carta! Mas, se eu tenho uma Quadra, posso não querer trocar nenhuma ou apenas uma, dependendo da estratégia – confesso que não sou um jogador de Poker 😉 No entanto, se eu não tenho nada (Maior Carta), posso tentar a sorte de várias formas! Os números na tabela indicam o quanto de “peso” aquela ação vai ter.
Mas, entenda, esses “pesos” não são determinados por nós! Temos que fazer o programa passar por uma fase de treinamento, onde ele vai tentar as ações em cada estado e verificar o resultado. Após a troca escolhida (ação), verificamos se a mão ficou melhor. Se sim, aumentamos esse “peso”. Se ficou pior, diminuímos esse “peso”.
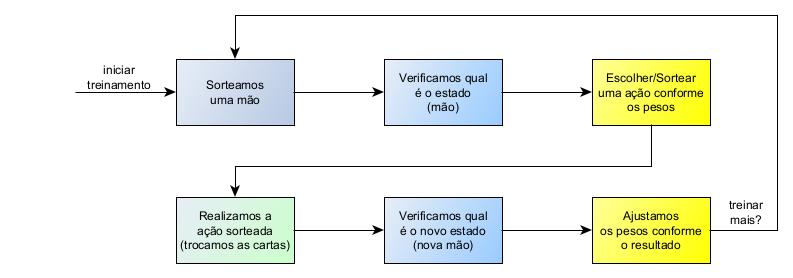
Perceba que, depois do treinamento, teremos uma tabela que vale ouro… 😉 Ela é um mapa para fazermos boas trocas de cartas e devemos gravá-la em algum lugar para usarmos posteriormente.
Implementação
Prometo que não vou entrar em tantos detalhes como no meu último post! 😉 Não vou me alongar no código do jogo de Poker em si, até porque o objetivo agora não é fazer todo o jogo, mas apenas a parte da troca de mão. Dessa forma, vou deixar o código pronto no meu GitHub para você dar uma olhada.
No entanto, gostaria de explicar alguns pontos:
1) A implementação que fiz foi bem rudimentar, baseado 100% na explicação que dei anteriormente. Não implementei TD, SARSA, Q-Learning (algoritmo que usei na implementação original do jogo para celular), nem nada disso. Vamos testar o conceito bruto! 😉 rs
2) As cartas estarão sempre ordenadas da maior para a menor na mão. Dessa forma, temos uma padronização para a escolha das cartas.
3) Eu limitei os pesos (do “tabelão”) para serem sempre maior que 1 para facilitar o cálculo das probabilidades dos pesos (a soma tem que ser maior que zero): probs = pesos / pesos.sum(). E coloquei um valor máximo também, para que não crescessem indefinidamente e começassem a enviesar alguma ação de troca específica (veja mais sobre isso no tópico Resultados mais à frente). Para você ter uma ideia mais completa, segue o trecho do código:
class EstrategiaTrocaRL(EstrategiaTroca):
MIN = 1
MAX = 5000
def _decidir_trocas(self, mao):
pesos_do_rank = self._tabela[mao.rank]
probs = pesos_do_rank / pesos_do_rank.sum()
return int(np.random.choice(len(pesos_do_rank), p=probs))
def registrar_resultado(self, rank_mao, indices, recompensa):
trocas = Mao.indices_to_trocas(indices)
peso = self._tabela[rank_mao, trocas]
if EstrategiaTrocaRL.MIN <= (peso + recompensa) <= EstrategiaTrocaRL.MAX:
self._tabela[rank_mao, trocas] += recompensa
4) A recompensa para empate coloquei como +1. Precisei fazer isso porque, no caso da melhor ação ser não trocar cartas, haverá “empate” (mão posterior é igual à mão anterior). Então precisamos dar uma recompensa positiva para esse caso. Compensei fazendo com que a recompensa para melhora de mão seja +2. No caso de piora, coloquei a recompensa como -1:
if mao_posterior > mao_anterior:
estrategia_troca_rl.registrar_resultado(mao_anterior, jogador.indices, 2)
elif mao_posterior < mao_anterior:
estrategia_troca_rl.registrar_resultado(mao_anterior, jogador.indices, -1)
else:
estrategia_troca_rl.registrar_resultado(mao_anterior, jogador.indices, 1)
5) No treinamento, eu forcei o aparecimento de cada tipo de mão! Malandragem! 😉 Isso porque, se fosse ficar esperando sair um Straight Flush, o algoritmo não iria ver tantos casos e o treinamento seria “fraco”, concorda?
Treinamento
O treinamento foi feito de duas formas (lembrando que, inicialmente, os pesos podiam assumir valores de 1 a 5000):
- Iniciando todos os pesos com 1
- Iniciando os pesos de forma aleatória
Foi possível observar a seguinte evolução em 1.000.000 de ciclos (episódios):
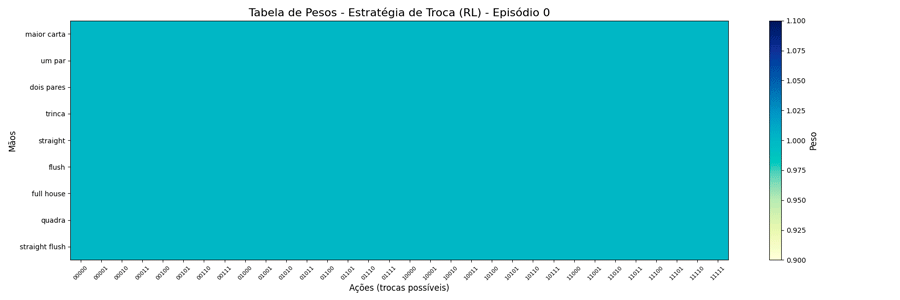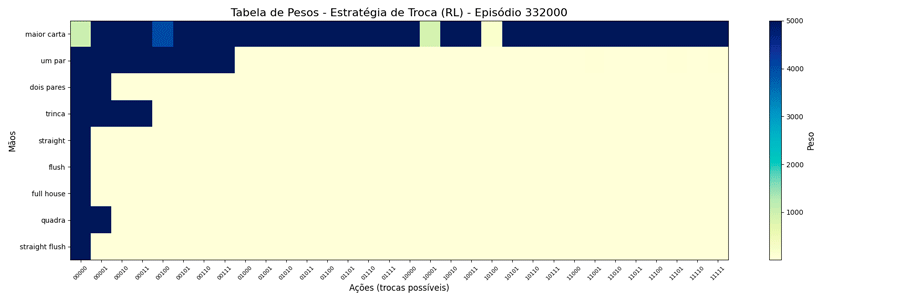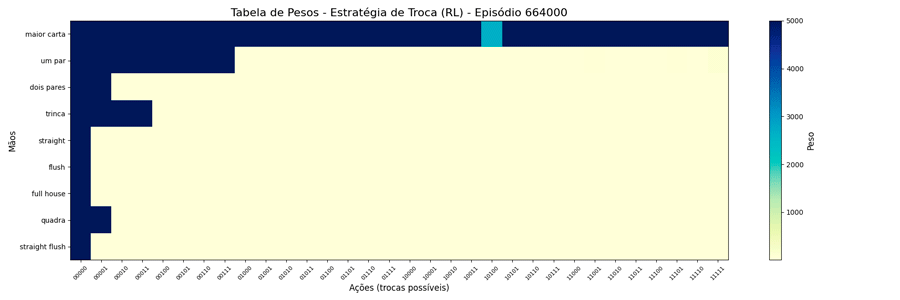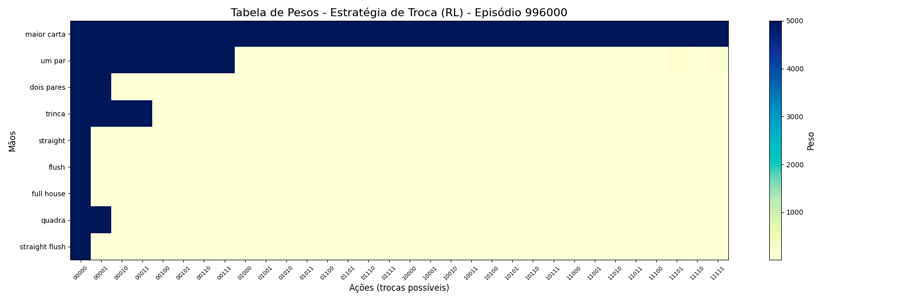
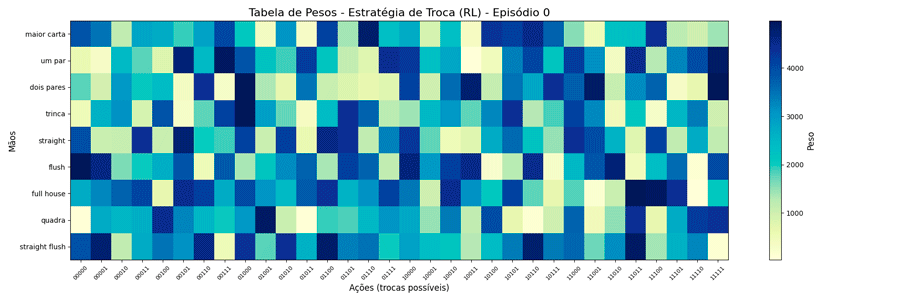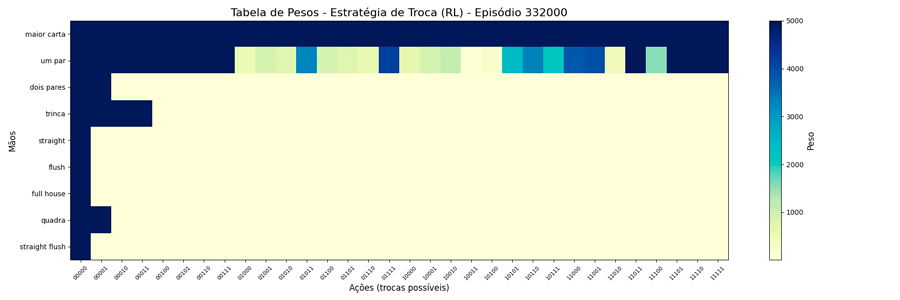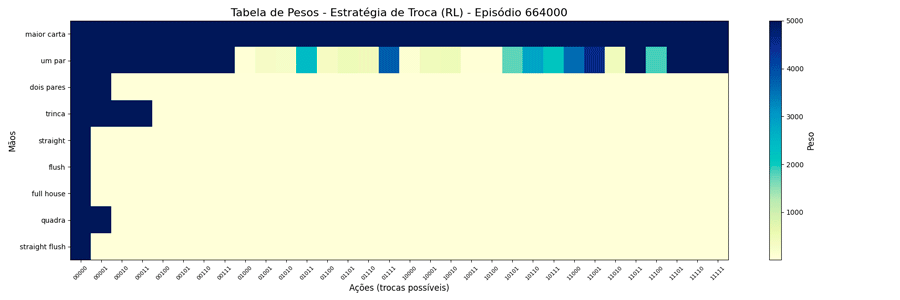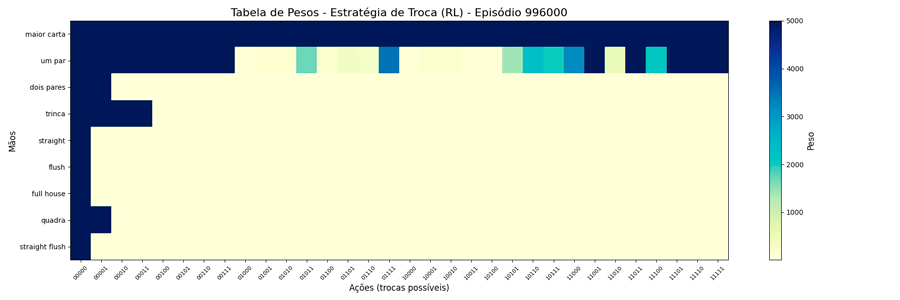
Interessante notar que surgiram estratégias “diferentes” para a troca de “um par”.
Estranhando isso, pensei em limitar o peso a um número menor, achando que, da forma como estava, poderia estar não tendo tempo de “regredir” para um valor menor quando houvesse piora nas cartas. A questão é: qual seria um bom número para este limite? Para responder a isso, pensei no caso de 1 ação vs as outras 31, qual seria o valor que corresponderia a 90% de chances dela ser escolhida?
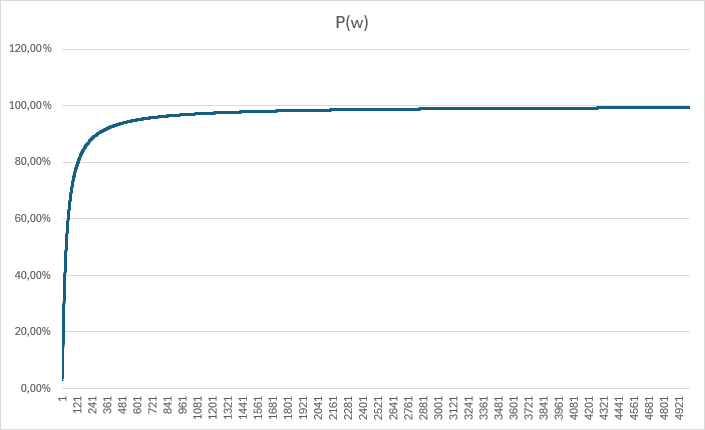
O gráfico foi só para ter o insight! rs A conta é P(w)=w/(w+31). Quero que P(w)=0.9. Fazendo as contas, chega-se que w=0.9*31/0.1 => w=279.
Dessa forma, alterei o MAX=279 e foi possível observar a seguinte evolução em 1.000.000 de ciclos (episódios):
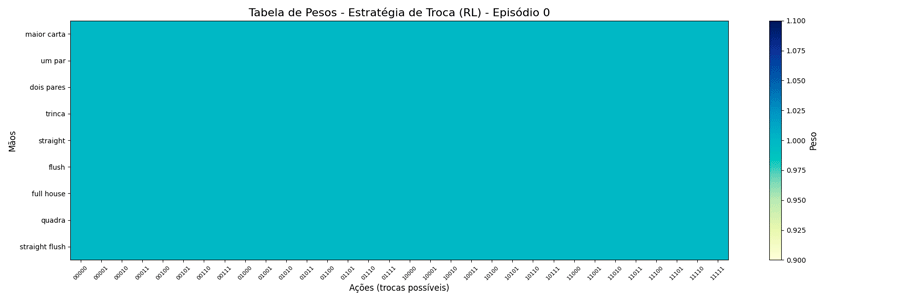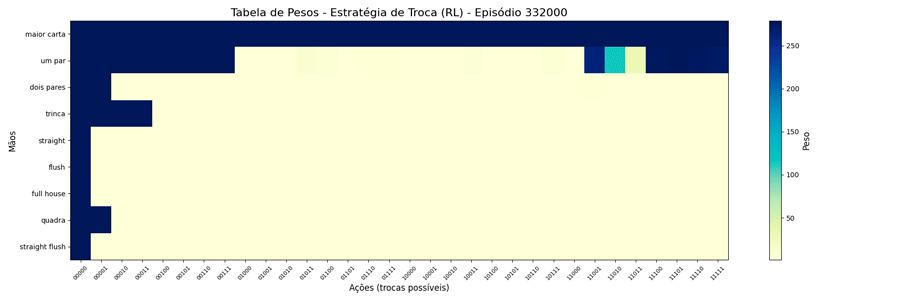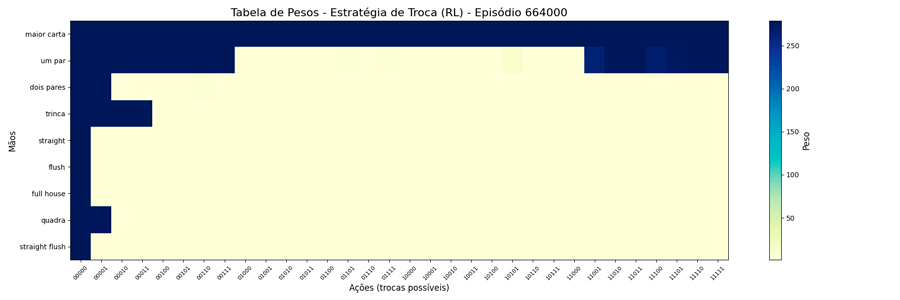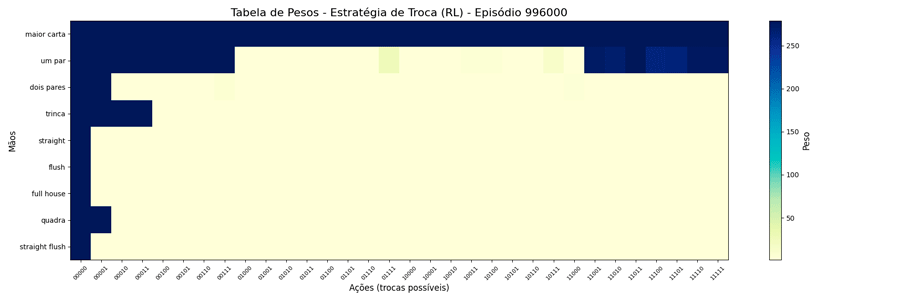
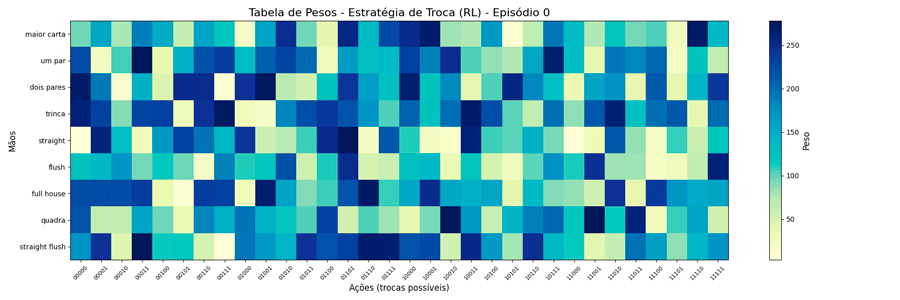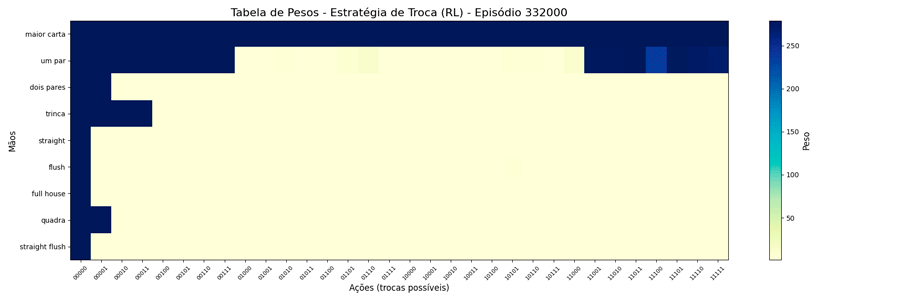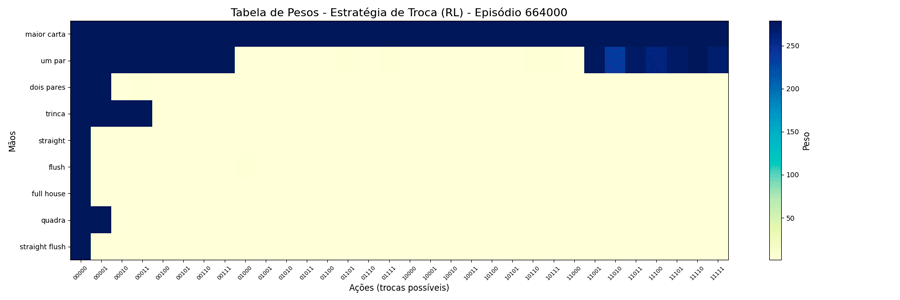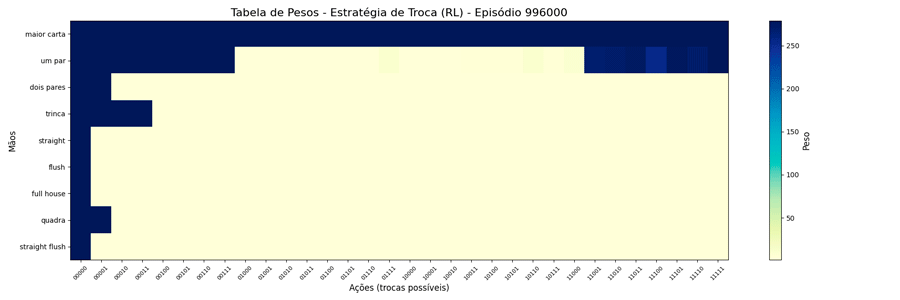
Uma vez que o peso máximo é menor, esses valores são atingidos mais rapidamente. E, também, as estratégias “diferentes” para a troca de “um par” se mantiveram (e foram reforçadas). Ponto a ser investigado em algum momento futuro…
Resultados
Após os treinamentos, coloquei todos para serem simulados e os seguintes resultados foram obtidos:
== Resultados para Troca Aleatória ==
empate: 50.7%
melhorou: 24.6%
piorou: 24.7%
== Resultados para RL Init 1 Max 279 ==
empate: 62.7%
melhorou: 27.0%
piorou: 10.4%
== Resultados para RL Init 1 Max 5000 ==
empate: 70.5%
melhorou: 29.3%
piorou: 0.2%
== Resultados para RL Init Aleatório Max 279 ==
empate: 62.7%
melhorou: 27.0%
piorou: 10.3%
== Resultados para RL Init Aleatório Max 5000 ==
empate: 62.0%
melhorou: 26.5%
piorou: 11.4%
Como já era esperado, os algoritmos treinados melhoram um pouco a mão de Poker, mas não muito! 24,6% na troca aleatória vs 29,3% no melhor treinamento (RL Init 1 Max 5000).
Agora, é interessantes notar que no melhor treinamento, o algoritmo conseguiu minimizar a piora na mão de Poker para apenas 0.2%! Talvez o título do post deveria ser alterado para “Usando Aprendizado por Reforço para não piorar uma mão de Poker”. 😉
O que achou do artigo? Quer contribuir? Comente conosco! E, claro, existe espaço para investigações como a questão dos valores máximos dos pesos e, também, seria interessante verificar valores diferentes para as recompensas. Além disso, seria legal testar com algoritmos clássicos e comparar com essa implementação mais root! O código está lá no GitHub. Que tal fazer um fork e uns PR’s? 😉
Até a próxima!

